Calculating the shorter angle of rotation in 2D

Here’s a really simple math problem in 2D games development that has a surprisingly complex solution. If I were to give you angles a and b, how would you calculate 1) the direction — that is, clockwise being positive; and anti-clockwise being negative — and 2) magnitude of the shorter angle of rotation from a to b?

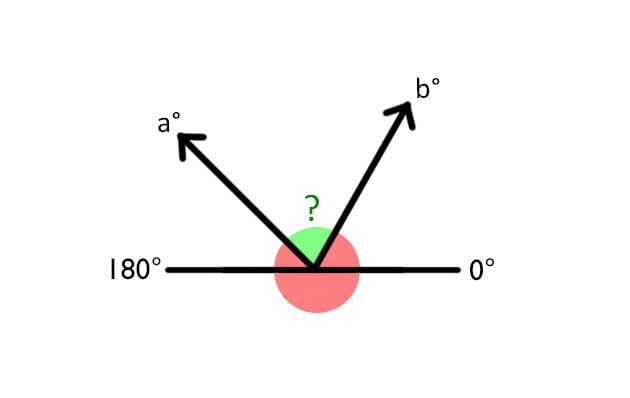
When you visualise it, both values seem so obvious; which was why I was so surprised I couldn’t figure it out. On the surface, it seems really simple — if you just take b – a, doesn’t it give you the solution?

(What looks like) the solution

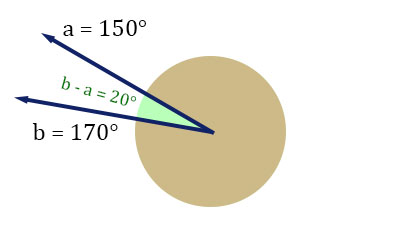
Here’s an example that illustrates how taking b – a can work:

$\mathrm{If\; we\; let\; a\; =\; 150°\; and\; b\; =\; 170°,}$ $\mathrm{b\; –\; a\; =\; 170°\; –\; 150°\; =\; 20°}$

The case above demonstrates that for the rotations pictured below, the formula correctly gives us a counter-clockwise rotation of 20° as the shorter angle of rotation.

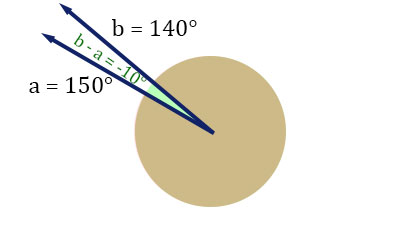
Conversely:

$\mathrm{If\; we\; let\; a\; =\; 150°\; and\; b\; =\; 140°,}$ $\mathrm{b\; –\; a\; =\; 140°\; –\; 150°\; =\; -10°}$

The case above demonstrates that for these other rotations pictured below, the formula correctly gives us a clockwise rotation of -10° as the shorter angle of rotation.

---

Article continues after the advertisement:

See discounted assets

---

The problem with angular values

When you begin to dig deeper, however, you will quickly find that things can get surprisingly complex problem for 2 reasons:

1. Angles loop around beyond 360°, so if a = 380° and b = 40°, we get 340° as the shorter angle of rotation. This is obviously wrong, because the shorter angle of rotation is never larger than 180°.
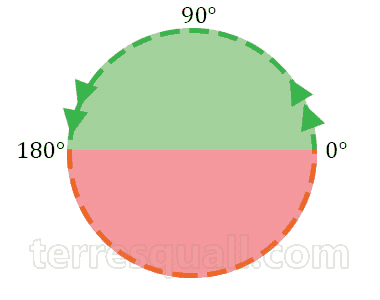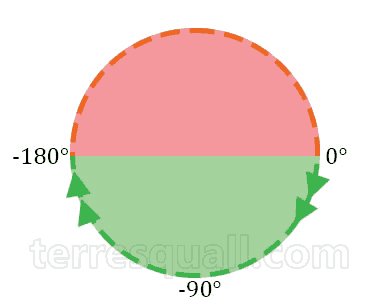
2. In most (i.e. 99%) game engines, the lower half of the circle goes from 0° to -180°, like radians do (refer to the picture below). Hence, if we were to consider cases like a = 160° and b = -160°, we will get 320° as the shorter angle of rotation.

The (actual) solution

Well, a – b actually works. Once you convert the result so that it is between -180° and 180° (or -π and π), that is. Here’s how you convert any angle into a value between -180° and 180°:

1. Firstly, if your result is already between -180° and 180°, then you ignore the following steps.
2. Next, convert your result into an angle between -360° and 360°. All you have to do is to modulo the result with 360, i.e. result % 360.
3. Finally, if your result is less than -180°, add 360° to it; otherwise, if it is more than 180°, subtract 360° from it.

Or, in short, expressed mathematically:

$\mathrm{f(x)}=\{\begin{array}{ll}\mathrm{sgn\; x\; \times \; 360°\; –\; |x|}& \mathrm{if\; |x|\; >\; 180}\\ x& \mathrm{if\; 0\; \ge \; |x|\; \le \; 180}\end{array}$

If that is hard to read, here’s a code snippet in C# that expresses the same thing:

float result = b - a; // Shorter angle of rotation.

// If our result's value is more than 180 or less than -180.
if(Mathf.Abs(result) > 180f)
	// Convert the value to be between -180 and 180.
	result = -Math.Sign(result) * (360f - Math.Abs(result));

Conclusion

Did the article help you figure out your angles? Or maybe you spotted some errors with our math? Feel free to leave us a comment below.

---

Article continues after the advertisement:

---